Complete set of commuting observables

In quantum mechanics, a complete set of commuting observables (CSCO) is a set of commuting operators whose eigenvalues completely specify the state of a system (Gasiorowicz 1974, p. 119).

For example, in the case of the hydrogen atom, the Hamiltonian H, the angular momentum L and its projection L_z along any arbitrary z axis form a CSCO (if one ignores the spin of the proton and of the electron as well as the movement of the center of mass).

Since each pair of observables in the set commutes, the observables are all compatible so that the measurement of one observable has no effect on the result of measuring another observable in the set. It is therefore not necessary to specify the order in which the different observables are measured. Measurement of the complete set of observables constitutes a complete measurement, in the sense that it projects the quantum state of the system onto a unique and known vector in the basis defined by the set of operators. This specifies the conditions for the preparation of a well-defined quantum state.

Also, the states which form the basis of the CSCO are completely defined by specifying the eigenvalues 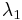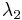$\lambda_1$ , $\lambda_2$ , ..., associated with each observable 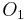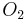$O_1$ , $O_2$ , ... of the CSCO. In the above example of the hydrogen atom, the basis states are defined by the quantum numbers $|n,l,m\rangle$ , and it is not necessary to include the wave function or the atomic orbital.

References

Gasiorowicz, Stephen (1974), Quantum Physics, New York: John Wiley & Sons, ISBN 978-0-471-29281-4 .